Not (Fido ate every cat)
(that takes care of the 'not'; now
we analyze 'Fido ate every cat')
Not (Every cat=x: (Fido ate x))
Not
(Every x: (if x is a cat then Fido ate x))
~
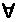 x(Cx->Afx)
x(Cx->Afx)
The difference between 'any' and 'every' can often be understood as a matter of scope. In general, 'any' tends to have wider scope than sentential connectives in the same sentence, while 'every' tends to have 'narrower scope. An example will help explain. In
Fido didn't eat every cat
the sentential connective 'not' operates on the whole sentence 'Fido ate every cat'. Our analysis reflects this by analyzing that connective first, then analyzing the rest of the sentence:
Not (Fido ate every cat)
(that takes care of the 'not'; now we analyze 'Fido ate every cat')
Not (Every cat=x: (Fido ate x))
Not (Every x: (if x is a cat then Fido ate x))
~x(Cx->Afx)
However, in
Fido didn't eat any cat
the quantifier 'any' has the entire sentence in its scope, and so we analyze 'any cat' first, then 'not':
Any cat=x: (Fido didn't eat x)
(Now we continue with the analysis of 'any cat':)
Any x: (if x is a cat then Fido didn't eat x)x(Cx->~Afx)
This example shows why our two-stage rewrite procedure is important: it's at the first rewrite stage that we decide whether to analyze the quantifier or the connective first. Here is a recipe rule:
This process also works when 'any' and 'every' are combined with conditionals. These sentences clearly don't mean the same thing:
If any professor is an idiot, then Smith is an idiot
If every professor is an idiot, then Smith is an idiot
Let's apply the recipe for 'any' and 'every' to show why they're different:
If any professor is an idiot, then Smith is an idiot
Any professor=x: (if x is an idiot, then Smith is an idiot)
Any x: (if x is a professor then (if x is an idiot then Smith is an idiot))x(Px->(Ix->Is))
If every professor is an idiot, then Smith is an idiot
If (every professor is an idiot) then (Smith is an idiot)
If (every professor=x: (x is an idiot)) then (Smith is an idiot)
(just to make it clearer, let's translate the main connective at this point:)
(every professor=x: (x is an idiot))->(Smith is an idiot)
(translating the left and right sides)
(every x: if x is a professor then x is an idiot)->(Smith is an idiot)x(Px->Ix) -> Is
'Only' usually indicates universal quantification, but the translation is different in an important way: the predicates in the original sentence wind up in different places in the final translation than they do with 'every.' Consider this example:
Only an idiot would do that
For simplicity's sake, let's treat '___ would do that' as a one-place predicate expression here. So, we can rewrite our sentence as:
Only an idiot=x: (x would do that)
A simple way to translate this is to turn 'only' into a universal quantifier 'every' followed by the sentential connective 'only if' placed after the bit of sentence we're translating, like this:
Every x: (x would do that only if x is an idiot)
As you'll remember from sentential logic, 'P only if Q' is just P->Q. So, using the translation scheme Ix= 'x is an idiot', Dx = 'x would do that', we can then translate this as:
x(Dx->Ix)
Here, then, is the recipe:
| FORM: | Only (predicate1) (predicate2) |
| FIRST REWRITE AS: | Only predicate1=x: (x (is) predicate2) |
| THEN REWRITE AS: | Every x: (x (is) (predicate2) only if x (is) (predicate1)) |
| Note the order of the predicates here! | |
| TRANSLATION SCHEME: | F=predicate1, G=predicate2 |
| TRANSLATION: | 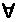 x(Gx->Fx) x(Gx->Fx) |
| Note the order of the predicates here! |
When several predicates occur together, treat them as a single predicate in the first rewrite and then break them up and connect with 'and':
Some ugly dog is on the porch
Some ugly dog=x: (x is on the porch)
Some x: ((x is an ugly dog) and x is on the porch)
Some x: ((x is ugly and x is a dog) and x is on the porch)x((Ux&Dx)&Px)
Every hairy cat is a loathsome nuisance
Every hairy cat=x: (x is a loathsome nuisance)
Every hairy cat=x: (x is loathsome and x is a nuisance)
Every x: (if x is a hairy cat then (x is loathsome and x is a nuisance))
Every x: (if (x is hairy and x is a cat) then (x is loathsome and x is a nuisance))x((Hx&Cx)->(Lx&Nx))
Predicates with relative clauses (involving 'which', 'that', 'who', etc., can be treated in the same way as compound predicates.
Every house that Jack built was overpriced
Every house that Jack built=x: (x was overpriced)
Every x: (if x is a house that Jack built then x was overpriced
Once you reach this point in the analysis, just turn the relative into 'and', then put 'x' (or whatever the variable is) in the appropriate place in the predicate expression. Now, in this case, the predicate expression is really '___ built ___': the first place is filled in with the name 'Jack', but the second is open. So, we rewrite as:
Every x: (if (x is a house and Jack built x) then x was overpriced
The translation, with scheme Hx='x is a house', Bxy='x built y', Ox='x was overpriced', and a='Jack', is:
((Hx&Bax)->Ox)
We've already introduced many-place predicates (predicates with more than one place), and a few previous examples contained such predicates (e.g. '___ ate ___'). With a many-place predicate, a quantifier can be attached to any place. With only a single quantifier involved, this is easy to handle: just make sure the quantifier's variable is in the right place. For these purposes, it's absolutely critical to be sure what translation scheme is being used, since only in that way can we tell which place following the predicate letter corresponds to which place in the English predicate expression. In the following two examples, we use the same translation scheme, namely
Translation scheme: Axy='x ate y', g='Godzilla'
Godzilla ate something
Something=x: Godzilla ate x
Some x: Godzilla ate xxAgx
Something ate Godzilla
Something=x: x ate Godzilla
Some x: x ate GodzillaxAxg
Some further examples (Cx='x is a cat', Mx='x is a monster', Axy='x ate y', g='Godzilla'):
Godzilla ate some cats
Some cat=x: (Godzilla ate x)
Some x: (x is a cat and Godzilla ate x)x(Cx&Agx)
Some monster ate Godzilla
Some monster=x: (x ate Godzilla)
Some x: (x is a monster and x ate Godzilla)x(Mx&Axg)
Translation scheme for these examples: Bxy='x bit y', Cx='x is a cat', f='Fido'
No cat bit Fido
No cat=x: (x bit Fido)
Every cat=x: not (x bit Fido)
Every x: (if x is a cat then not (x bit Fido))x(Cx->~Bxf)
Fido bit no cat
No cat=x: (Fido bit x)
Every cat=x: not (Fido bit x)
Every x: (if x is a cat then not (Fido bit x))x(Cx->~Bfx)
Things get more complicated when we add a second quantifier. The basic rule is to analyze quantifiers one at a time, in order from left to right:
Some monster ate all the cats
Some monster=x: (x ate all the cats)
Some x: (x is a monster and (x ate all the cats))
Some x: (x is a monster and (every cat=y: (x ate y)))
(Notice what happened here: we analyzed 'x ate all the cats' right where it is.)
Some x: (x is a monster and (every y: (if y is a cat then x ate y)))x(Mx&
y(Cy->Axy))
Compare this to:
Some cat ate all the monsters
Some cat=x: (x ate all the monsters)
Some x: (x is a cat and (x ate all the monsters))
Some x: (x is a cat and (every monster=y: (x ate y)))
Some x: (x is a cat and (every y: (if y is a monster then x ate y)))x(Cx&
y(My->Axy))
And also to:
Every monster ate some cats
Every monster=x: (x ate some cats)
Every x: (if x is a monster then (x ate some cats))
Every x: (if x is a monster then (some cat=y: (x ate y)))
(Compare this with the same stage in the previous two examples.)
Every x: (if x is a monster then (some y: (y is a cat and x ate y)))x(Mx->
y(Cy&Axy))