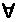 x((Px&
x((Px&
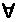 y(Py->Lxy))->Lxa)
y(Py->Lxy))->Lxa)We can combine the previous methods to translate relative clauses containing quantifiers.
Everyone who loves everyone loves GeorgeThe subject of this sentence is "everyone who loves everyone"; it contains the relative clause "who loves everyone". We can apply the preceding recipes step by step:
Of everyone who loves everyone=x: x loves George
Of every x: if x is a person who loves everyone then x loves George
Of every x: if (x is a person and x loves everyone) then x loves George
Of every x: if (x is a person and of everyone=y: x loves y) then x loves George
Of every x: if (x is a person and of every y: if y is a person then x loves y) then x loves George
Further examples:x((Px&
y(Py->Lxy))->Lxa)
A dog that bit Fluffy bit me
Of some dog that bit Fluffy=x: x bit me
Of some x: x is a dog that bit Fluffy and x bit me
Of some x: x is a dog and x bit Fluffy and x bit me
x(Dx&Bxa&Bxb)
No dog that bit Fluffy bit me
Of no dog that bit Fluffy=x: x bit me
Of every dog that bit Fluffy=x: not(x bit me)
Of every x: if (x is a dog that bit Fluffy) then not (x bit me)
Of every x: if (x is a dog and x bit Fluffy) then not (x bit me)
x((Dx&Bxa)->~Bxb)
I bite every dog that bites me
Of every dog that bites me=x: I bite x
Of every x: if (x is a dog that bites me) then I bite x
Of every x: if (x is a dog and x bites me) then I bite x
x((Dx&Bxb)->Bbx)
Every dog that bit a cat was bitten by a rat
Of every dog that bit a cat=x: x was bitten by a rat
Of every x: if x is a dog that bit a cat then x was bitten by a rat
Of every x: if (x is a dog and of some (a) cat=y: x bit y) then x was bitten by a rat
Of every x: if (x is a dog and (of some y: y is a cat and x bit y)) then x was bitten by a rat
Of every x: if (x is a dog and (of some y: y is a cat and x bit y)) then of some rat = z: x was bitten by z
Of every x: if (x is a dog and (of some y: y is a cat and x bit y)) then (of some z: z is a rat and x was bitten by z)
x ((Dx&
y (Cy&Bxy))->
z (Rz&Bzx))
(Note that Bxy="x bit y" and also "y was bitten by x")
A dog that bit a cat bit a man that wore a hat
Of some dog that bit a cat =x: x bit a man that wore a hat
Of some x: x is a dog that bit a cat and x bit a man that wore a hat
Of some x: (x is a dog and x bit a cat) and (x bit a man that wore a hat)
Of some x: (x is a dog and of some cat=y: x bit y) and (x bit a man that wore a hat)
Of some x: (x is a dog and of some y: y is a cat and x bit y) and (x bit a man that wore a hat)
Of some x: (x is a dog and of some y: y is a cat and x bit y) and (of some man that wore a hat=z: x bit z)
Of some x: (x is a dog and of some y: y is a cat and x bit y) and (of some z: z is a man that wore a hat and x bit z)
Of some x: (x is a dog and of some y: y is a cat and x bit y) and (of some z: z is a man and z wore a hat and x bit z)
Of some x: (x is a dog and of some y: y is a cat and x bit y) and (of some z: z is a man and (of some hat=w: z wore w) and x bit z)
Of some x: (x is a dog and of some y: y is a cat and x bit y) and (of some z: z is a man and (of some w: w is a hat and z wore w) and x bit z)
x((Dx&
y(Cy& Bxy))&
z(Mz&
w((Hw&Wzw)&Bxz)))
Fluffy ate every mouse Snookums didn't eatSentences built like this can get remarkably involved:
(making it more explicit:) Fluffy ate every mouse thatSnookums didn't eat
Of every mouse thatSnookums didn't eat=x: Fluffy ate x
Of every x: if x is a mouse thatSnookums didn't eat then Fluffy ate x
Of every x: if x is a mouse and Snookums didn't eat x then Fluffy ate x
x ((Mx&~Aax)->Abx)
A dog bit a cat:x(Dx&
y(Cy&Bxy))
A dog a rat bit bit a cat:x(Dx&
y((Ry&Byx)&
z(Cz&Bxz)))
A dog a rat a snake bit bit bit a cat:x(Dx&
y(Ry&
z((Sz&Bzy)&Byx)&
w(Cw&Bxw)))
A dog a rat a cat a baby bit bit bit expired
Plurals in constructions like these often function as universal quantifiers:
People like dogs
People dogs like like dogs
Fido is a schnauzer and Rover is a schnauzerThe second sentence, however, is just a simple predication with a two-place predicate "__and__are littermates". If you rewrite it as
Fido is a littermate and Rover is a littermate,the result no longer means the same thing as the original. Other examples:
John and Mary are married [i.e. to each other]This gives us a useful test: if we can rewrite a sentence containing a compound subject (two names connected with "and") as an explicit conjunction without changing its meaning, then the original sentence was a conjunction; if rewriting it changes its meaning, then the original sentence involved a two-place predicate.
Alice and Anita are sisters
Godzilla and Mothra were engaged in mortal combat
Bush and Clinton were opponents
When we apply this to sentences with quantifiers, the same test will continue to work. First, an example involving conjunction:
All dogs and cats are mammalsNext, an example involving a two-place predicate:
=All dogs are mammals and all cats are mammals
=x(Dx->Mx)&
x(Cx->Mx)
All dogs and cats are enemiesThe rewriting test shows that this sentence is not a conjunction. But how do we translate it? We need to introduce a new technique. The subject of this sentence, logically speaking, is actually all dog-cat pairs, that is, every pair xy where x is a dog and y is a cat. Let's express this as follows:
=All dogs are enemies and all cats are enemies? NO
Of every dog and cat=xy: x and y are enemiesWe can then finish translating this using our usual techniques:
Of (every dog=x, every cat=y): x and y are enemies
Of every x: if x is a dog then of every y: if y is a cat then x and y are enemiesWe can avail ourselves of a little logical magic to make this simpler. It just happens to be the case that
x(Dx->
y(Cy->Exy))
is equivalent tox(Dx->
y(Cy->Exy))
which in turn is equivalent tox
y(Dx->(Cy->Exy))
which you could also write asx
y(Dx&Cy->Exy)
So, we have a recipe for translating sentences of the form "All Fs and Gs are Hs" when 'H' is really a two-place predicate.xy(Dx&Cy->Exy)
Similar methods work with existential quantifiers:
Some dogs and cats are house pets
=Some dogs are house pets and some cats are house pets
of some x(x is a dog and x is a house pet) and of some y(y is a cat and y is a house pet)x(Dx&Hx)&
y(Cy&Hy)
Some dogs and cats are friendsThis also can be made a little neater with some logical tricks: it's equivalent to
=Some dogs are friends and some cats are friends? NO
Of some dog and cat=xy: x and y are friends
Of some x: x is a dog and of some y: y is a cat and x and y are friends
x(Dx&
y(Cy&Fxy))
xy(Dx&Cy&Fxy)
However, most logicians will give rather different translations from the more complex ones here. Often, they're just as long but have a difference in order (for one thing, the quantifiers are likely to come in strings at the beginning); in some cases, they may be much shorter. These different translations will be equivalent to the ones reached methodically here. Generally, it is a complex business to determine whether two formulas are equivalent: to prove equivalence, you would need to show that each could be deduced from the other. However, it might be useful to take note here of some equivalences that hold generally.