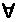
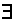
In addition to names, predicate letters, and the connectives of sentential logic, our symbolic language for predicate logic contains two other types of symbol: quantifiers and variables. These always go together: in a wff, every quantifier must be associated with a variable, and every occurrence of a variable must be associated with a quantifier.
Variables are the last six letters of the alphabet, with or without subscripts (we allow ourselves to have as many of these as we need:
| VARIABLES | u, v, w, x, y, z, u1, v1, w1, x1, y1, z1, u2, v2, w2, x2, y2, z2, ... |
There are two quantifiers, each of which has its own name:
| The Universal Quantifier | 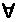
|
| The Existential Quantifier | 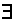
|
Don't confuse variables with names: variables are lower-case letters from the end of the alphabet (u, v, w, x, y, z), while names are lower case letters from the beginning of the alphabet (a, b, c, d).
In a wff:
The process of turning English sentences into symbolic notation is considerably more complicated than the process of translating into sentential-logic formulas. One reason the process is sometimes confusing is that there are usually a number of equally correct ways of translating the same English sentence. What I mean by "equally correct" is that the different translations are actually logically equivalent to one another, even though they may look very different. With lots of possibilities to choose from, it's sometimes hard to know where to begin.
So, here are several recipes for translating a variety of English sentence patterns into wffs. Like recipes, they usually work but sometimes fail, and if you have some experience in translating you can often find simpler translations. However, they have the advantage of being methodical.
In order to explain these recipes, I need to introduce another notion. Previously, we associated predicate letters with English predicate expressions, which are sentences in which occurrences of names have been replaced by blank places:'___ is a dog', '___ ate ___'. However, there are many uses of predicate expressions in English in which this form is not so obvious. Consider these two sentences:
In the first sentence, we can see clearly the predicate expression '___ is a dog,' with its bnalk space filled in with the name 'Rover'. However, in the second example, we have the word 'dog' but no obvious blank spaces associated with it. We explain this as follows: in sentence 2, the predicate expression '___ is a dog' is still present, but implicitly. What the sentence says is actually two things: (1) something is a dog and (2) it's barking. To put this more precisely, the sentence says:
Of some x: x is a dog and x is barking
This rewriting of the sentence does contain the predicate expression '___ is a dog', in addition to the predicate expression '___ is barking.' Therefore, we can regard it as also present implicitly in the original sentence 'Some dog is barking.' In what follows, we'll do a great deal of this sort of rewriting, moving between fully-expressed predicate expressions like '___ is a dog' and more abbreviated but equivalent ones like 'dog'.
For convenience, we'll use the term predicate for any English-language expression that can be regarded as a predicate expression. This includes both '___ is a dog' and the shorter form 'dog.' We will also treat 'dog' and '___is a dog' as just two different forms of the same predicate. We also regard '___ is a dog' as its standard form, and we turn other forms into this in translation: 'dog', 'dogs', etc.
| FORM: | Some (predicate1) (predicate2) |
| FIRST REWRITE AS: | Some predicate1=x: (x (is) predicate2) |
| THEN REWRITE AS: | Some x: (x (is) (predicate1) and x (is) (predicate2)) |
| TRANSLATION SCHEME: | F=predicate1, G=predicate2 |
| TRANSLATION: | 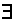 x(Fx&Gx) x(Fx&Gx)
|
At this stage, the first rewrite may seem unnecessary. Later on, we'll see that it is an important step in dealing with complex cases.
Some examples:
| EXAMPLE: | Some dog is barking |
| FIRST REWRITE AS: | Some dog=x: (x is barking) |
| REWRITE AS: | Some x: (x is a dog and x is barking) |
| TRANSLATION SCHEME: | Dx=x is a dog, Gx=x is barking |
| TRANSLATION: | 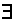 x(Dx&Bx) x(Dx&Bx)
|
Other forms using this recipe:
| Plural: | Some dogs are barking |
| Indefinite article: | A dog is barking |
We can also include here the quantifier words 'someone,' somebody'.
| FORM: | Every (predicate1) (predicate2) |
| FIRST REWRITE AS: | Every predicate1=x: (x predicate2 |
| THEN REWRITE AS: | Every x: (if x (is) (predicate1) then x (is) (predicate2)) |
| TRANSLATION SCHEME: | F=predicate1, G=predicate2 |
| TRANSLATION: | 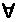 x(Fx->Gx) x(Fx->Gx)
|
Some examples:
| EXAMPLE: | Every dog pants |
| Every dog=x: (x pants) | |
| REWRITE AS: | Every x: (if x is a dog then x pants |
| TRANSLATION SCHEME: | Dx=x is a dog, Px=x pants |
| TRANSLATION: | 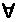 x(Dx->Px) x(Dx->Px)
|
Some other equivalent patterns using this recipe:
| All: | All dogs pant |
| Each: | Each dog pants |
| Plurals alone: | Dogs pant (Note: these are often ambiguous) |
| Any: | Any dog pants |
'Everyone,' 'anyone', 'everybody', anybody' function in the same way.
| FORM: | No (predicate1) (predicate2) |
| FIRST REWRITE AS: | Every predicate1=x: not (x predicate2) |
| REWRITE AS: | Every x: (if x (is) (predicate1) then not x (is) (predicate2)) |
| TRANSLATION SCHEME: | F=predicate1, G=predicate2 |
| TRANSLATION: | 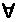 x(Fx->~Gx) x(Fx->~Gx)
|
Here., the first rewrite lets us put the sentence into the same pattern as a simple universal quantification, and the rest of the translation proceeds as with 'every.' This shows a little bit of the point of rewriting in two stages, but its real value will become evident later.
Some examples:
| EXAMPLE: | No dog sweats |
| FIRST REWRITE AS: | Every dog = x: not (x sweats) |
| THEN REWRITE AS: | Every x: (if x is a dog then not (x sweats)) |
| TRANSLATION SCHEME: | Dx=x is a dog, Sx=x sweats |
| TRANSLATION: | 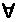 x(Dx->~Sx) x(Dx->~Sx)
|
Some other equivalent patterns using this recipe:
| Plurals with negation: | Dogs don't sweat |
'Nobody' and 'no one' can be translated similarly.
Sentences often contain quantifiers and sentential connectives in combination. Sometimes, this is straightforward: quantifications are sentences too, and they can be combined with connectives.
One example:
Some dogs are ugly, but Fido isn't
(Some dogs are ugly) and not(Fido is ugly)
(Some dog=x:(x is ugly) and not (Fido is ugly)
(Some x: (x is a dog and x is ugly and not (Fido is ugly)x(Dx&Ux)&~Uf
Translation scheme: Dx=x is a dog, Ux= x is ugly, f=Fido
Another example:
Some dogs are ugly, but all dogs are loveable
(Some dogs are ugly) but (all dogs are loveable)
(Some dog=x: x is ugly) but (Every dog=x: x is loveable)
(Some x: x is a dog and x is ugly) but (Every x: if x is a dog then x is loveable)x(Dx&Ux)&
x(Dx->Lx)
In the last example, notice that the 'x' in the left conjunct
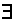 (Dx&Ux) has
nothing to do with the 'x' in the right conjunct
(Dx&Ux) has
nothing to do with the 'x' in the right conjunct
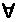 (Dx->Lx): these are two
separate wffs. However, although it's perfectly correct to use the same
variable in connection with different quantifiers in a case like this, it might
be clearer to pick different variables:
(Dx->Lx): these are two
separate wffs. However, although it's perfectly correct to use the same
variable in connection with different quantifiers in a case like this, it might
be clearer to pick different variables:
y(Dy&Uy)&
x(Dx->Lx)
Since quantifications are sentences, they can be denied, just like any other sentence. With simple universal quantifications, one way to do this is particularly clear: put a 'not' at the beginning:
Not every dog is vicious
not (every dog is vicious)
~(every x: if x is a dog then x is vicious)
~x(Dx->Vx)
'Not all' works the same way as 'not every'. Notice that there are no
parentheses around 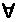 x(Dx->Vx):
we only need parentheses around the open form Dx->Vx.
x(Dx->Vx):
we only need parentheses around the open form Dx->Vx.
You'll remember from sentential logic that in English, the word that makes a sentence a negation is usually somewhere in the middle of it, not at the beginning: 'John is not tall', 'Fido doesn't have fleas.' With quantifications, however, these combinations usually take on a different meaning. Consider this sentence:
Some dogs aren't ugly
You might think this is simply the negation of 'Some dogs are ugly' and
translate it ~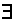 x(Dx&Ux).
However, if these two sentences are denials of each other, then the sentence
'Some dogs are ugly and some dogs aren't ugly' should be self-contradictory,
just like 'Fido is ugly and Fido isn't ugly.' But it obviously isn't: the truth
is, some dogs are ugly and some dogs aren't. What went
wrong? The answer is that the negation in 'Some dogs aren't ugly' is actually
attached only to the second predicate. This comes out nicely in our two-stage
method of rewriting:
x(Dx&Ux).
However, if these two sentences are denials of each other, then the sentence
'Some dogs are ugly and some dogs aren't ugly' should be self-contradictory,
just like 'Fido is ugly and Fido isn't ugly.' But it obviously isn't: the truth
is, some dogs are ugly and some dogs aren't. What went
wrong? The answer is that the negation in 'Some dogs aren't ugly' is actually
attached only to the second predicate. This comes out nicely in our two-stage
method of rewriting:
Some dogs aren't ugly
Some dog=x: (x isn't ugly)
Some x: (x is a dog and x isn't ugly)x(Dx&~Ux)
This same form of translation will help us deal with complicated predicates:
Some dogs are ugly, mean, and nasty
Some dog=x: (x is ugly, mean, and nasty)
Some dog=x: (x is ugly and x is mean and x is nasty)
Some x: (x is a dog and (x is ugly and x is mean and x is nasty))x(Dx&(Ux&(Mx&Nx)))
Every dog is slimy, icky, or awful
Every dog=x:(x is slimy, icky, or awful)
Every dog=x:(x is slimy or x is icky or x is awful)
Every x: (if x is a dog then (x is slimy or x is icky or x is awful))x(Dx->(Sx v (Ix v Ax)))
Sometimes, we find sentential connectives in the first predicate, as well. In these cases, the best strategy is usually to take these connectives as having larger scope than any quantifiers:
Some dogs and cats are wimps
(Some dogs are wimps) and (some cats are wimps)
(Some dog=x: (x is a wimp)) and (some cat=y: (y is a wimp))
(Some x: (x is a dog and x is a wimp) and (some y: (y is a cat and y is a wimp))x(Dx & Wx) &
y(Cy & Wy)
All dogs and cats are mammals
(All dogs are mammals) and (all cats are mammals)
Every dog=x:(x is a mammal) and (every cat=y: (y is a mammal))
(every x: (if x is a dog then x is a mammal)) and (every y: (if y is a cat then y is a mammal))x(Dx->Mx) &
y(Cy->My)
Be careful, however, about cases in which 'and' really indicates a two-place predicate:
All dogs and cats are enemies
This really contains the two-place predicate expression '___ and ___ are enemies.' Compare 'Fred and Ferd are brothers': this doesn't (usually) mean 'Fred is a brother and Ferd is a brother', but rather that Fred is Ferd's brother (and conversely). We'll return to these later.
Above, we listed 'any' along with 'every' and 'all' as one of the words used in forming simple universal quantifications. In combination with sentential connectives, however, 'any' and 'every' don't behave alike. Compare these two sentences:
Fido didn't eat every cat
Fido didn't eat any cat
The first sentence leaves room for a lot of cat-eating on Fido's part ("Yes,
Ms. Jones, I realize Fido's been eating your cats again today, but he's getting
better: after all, he didn't eat every cat"), but the second says
that he's totally innocent. But the only difference is that the first contains
'every' where the second contains 'any'. How does that work?