Lecture Notes: Section 3.4

Section 3.4: Sequents, Theorems, and Derived Rules

Comment: There are eight valid sequents that show the various possible patterns of quantifier exchange, which capture the logical relations between the two quantifiers and negation. As with all valid sequents, these can be used as derived rules. And because they are so useful, we give them a name them explicitly:

(S131)	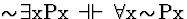$\sim \! \exists \mathrm{xPx}\, \dashv \vdash \, \forall \mathrm{x}\! \sim \! \mathrm{Px}$	Quantifier Exchange

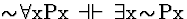(S130)	$\sim \! \forall \mathrm{xPx}\, \dashv \vdash \, \exists \mathrm{x}\! \sim \! \mathrm{Px}$	QE

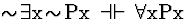(S133)	$\sim \! \exists \mathrm{x}\! \sim \! \mathrm{Px}\, \dashv \vdash \, \forall \mathrm{xPx}$	QE

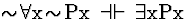(S132)	$\sim \! \forall \mathrm{x}\! \sim \! \mathrm{Px}\, \dashv \vdash \, \exists \mathrm{xPx}$	QE

Comment: The QE derived rules enable you to ``push'' an initial tilde through an adjacent quantifier-- where the ``effect'' of so pushing the tilde is to turn the quantifier to its counterpart, i.e., existential quantifiers turn to universals and universals to existentials. (This is what we see in the ``left to right'' direction of the above 2-way sequents.) Similarly, the operation can be reversed: a tilde to the right of an adjacent initial quantifier can be ``pulled'' through the quantifier, and the effect is again to turn the quantifier to its counterpart.

Proof of S131, left to right

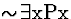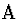1	(1)	$\sim \! \exists \mathrm{xPx}$	$\mathrm{A}$
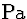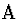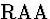2	(2)	$\mathrm{Pa}$	$\mathrm{A}$ (for $\mathrm{RAA}$ )
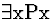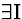2	(3)	$\exists \mathrm{xPx}$	2 $\exists \mathrm{I}$
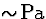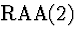1	(4)	$\sim \! \mathrm{Pa}$	1,3 $\mathrm{RAA}(2)$
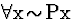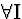1	(5)	$\forall \mathrm{x}\! \sim \! \mathrm{Px}$	4 $\forall \mathrm{I}$

Two proofs of S131, right to left

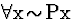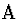1	(1)	$\forall \mathrm{x}\! \sim \! \mathrm{Px}$	$\mathrm{A}$
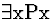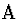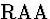2	(2)	$\exists \mathrm{xPx}$	$\mathrm{A}$ (for $\mathrm{RAA}$ )
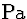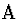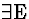3	(3)	$\mathrm{Pa}$	$\mathrm{A}$ (for $\exists \mathrm{E}$ )
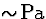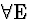1	(4)	$\sim \! \mathrm{Pa}$	1 $\forall \mathrm{E}$
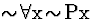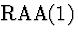3	(5)	$\sim \! \forall \mathrm{x}\! \sim \! \mathrm{Px}$	3,4 $\mathrm{RAA}(1)$
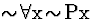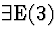2	(6)	$\sim \! \forall \mathrm{x}\! \sim \! \mathrm{Px}$	2,5 $\exists \mathrm{E}(3)$
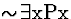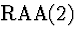1	(7)	$\sim \! \exists \mathrm{xPx}$	1,6 $\mathrm{RAA}(2)$

Comment: Note that our rules allow you to ``discharge'' a primary assumption in an RAA proof (line (5)). What this indicates here is simply that the assumption in question is incompatible with the sentences indicated in the assumption set. 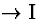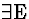However, this feature of the system might seem unintuitive if you (as I) like to think of discharged assumptions as temporary assumptions that have been discarded because they have served their purpose (in RAA, $\rightarrow \mathrm{I}$ , or $\exists \mathrm{E}$ ). 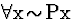Consequently, people of this mindset might prefer the following proof, in which a copy of the primary assumption $\forall \mathrm{x}\! \sim \! \mathrm{Px}$ is explicitly assumed (line (3) for RAA and later discharged (line 6).

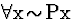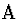1	(1)	$\forall \mathrm{x}\! \sim \! \mathrm{Px}$	$\mathrm{A}$
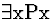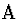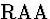2	(2)	$\exists \mathrm{xPx}$	$\mathrm{A}$ (for $\mathrm{RAA}$ )
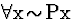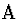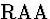3	(3)	$\forall \mathrm{x}\! \sim \! \mathrm{Px}$	$\mathrm{A}$ (for $\mathrm{RAA}$ )
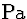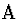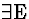4	(4)	$\mathrm{Pa}$	$\mathrm{A}$ (for $\exists \mathrm{E}$ )
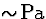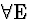3	(5)	$\sim \! \mathrm{Pa}$	3 $\forall \mathrm{E}$
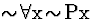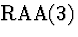4	(6)	$\sim \! \forall \mathrm{x}\! \sim \! \mathrm{Px}$	4,5 $\mathrm{RAA}(3)$
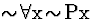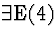2	(7)	$\sim \! \forall \mathrm{x}\! \sim \! \mathrm{Px}$	2,6 $\exists \mathrm{E}(4)$
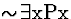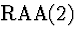1	(8)	$\sim \! \exists \mathrm{xPx}$	1,7 $\mathrm{RAA}(2)$

Comment: There are a number of valid sequents that, roughly, show how quantifiers are effected by altering their scopes. These are called Confinement rules.

(S134)	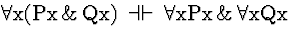$\forall \mathrm{x}(\mathrm{Px}\, \&\, \mathrm{Qx})\, \dashv \vdash \, \forall \mathrm{xPx}\, \&\, \forall \mathrm{xQx}$	Confinement

(S135)	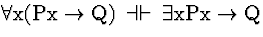$\forall \mathrm{x}(\mathrm{Px}\rightarrow \mathrm{Q})\, \dashv \vdash \, \exists \mathrm{xPx}\rightarrow \mathrm{Q}$	Conf

(S136)	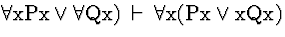$\forall \mathrm{xPx}\vee \forall \mathrm{Qx})\, \vdash \, \forall \mathrm{x}(\mathrm{Px}\vee \mathrm{xQx})$	Conf

(S137)	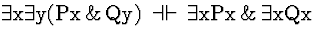$\exists \mathrm{x}\exists \mathrm{y}(\mathrm{Px}\, \&\, \mathrm{Qy})\, \dashv \vdash \, \exists \mathrm{xPx}\, \&\, \exists \mathrm{xQx}$	Conf

(S138)	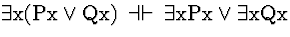$\exists \mathrm{x}(\mathrm{Px}\vee \mathrm{Qx})\, \dashv \vdash \, \exists \mathrm{xPx}\vee \exists \mathrm{xQx}$	Conf

(S139)	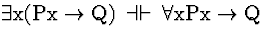$\exists \mathrm{x}(\mathrm{Px}\rightarrow \mathrm{Q})\, \dashv \vdash \, \forall \mathrm{xPx}\rightarrow \mathrm{Q}$	Conf

(S140)	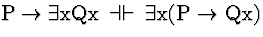$\mathrm{P}\rightarrow \exists \mathrm{xQx}\, \dashv \vdash \, \exists \mathrm{x}(\mathrm{P}\rightarrow \mathrm{Qx})$	Conf

(S141)	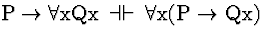$\mathrm{P}\rightarrow \forall \mathrm{xQx}\, \dashv \vdash \, \forall \mathrm{x}(\mathrm{P}\rightarrow \mathrm{Qx})$	Conf

Comment: The QE rules and the Confinement rules indicate that any sentence may be converted into an equivalent sentence in which no connective is outside the scope of any quantifier in the formula. Such a sentence, called a prenex sentence, has all its quantifiers in a row at the beginning of the sentence.

About this document ...

Chris Menzel

22 April 1998