Section 3.4: Sequents,
Theorems, and Derived Rules
Comment: There are
eight valid sequents that show the various possible patterns of quantifier
exchange, which capture the logical relations between the two quantifiers
and negation. As with all valid sequents, these can be used as derived
rules. And because they are so useful, we give them a name them explicitly:
| (S131) |
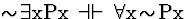 |
Quantifier Exchange |
|
|
|
| |
|
|
|
|
|
| (S130) |
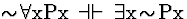 |
QE |
|
|
|
| |
|
|
|
|
|
| (S133) |
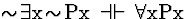 |
QE |
|
|
|
| |
|
|
|
|
|
| (S132) |
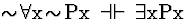 |
QE |
|
|
|
Comment: The QE
derived rules enable you to ``push'' an initial tilde through an adjacent
quantifier-- where the ``effect'' of so pushing the tilde is to turn the
quantifier to its counterpart, i.e., existential quantifiers turn to universals
and universals to existentials. (This is what we see in the ``left to right''
direction of the above 2-way sequents.) Similarly, the operation can be
reversed: a tilde to the right of an adjacent initial quantifier can be
``pulled'' through the quantifier, and the effect is again to turn the
quantifier to its counterpart.
Proof of S131, left to
right
| 1 |
(1) |
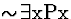 |
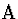 |
| 2 |
(2) |
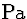 |
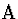 (for
(for 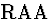 ) ) |
| 2 |
(3) |
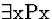 |
2 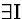 |
| 1 |
(4) |
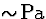 |
1,3 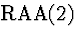 |
| 1 |
(5) |
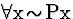 |
4 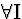 |
Two proofs of S131, right
to left
| 1 |
(1) |
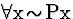 |
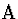 |
| 2 |
(2) |
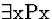 |
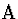 (for
(for 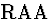 ) ) |
| 3 |
(3) |
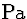 |
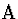 (for
(for 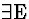 ) ) |
| 1 |
(4) |
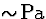 |
1 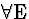 |
| 3 |
(5) |
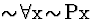 |
3,4 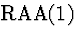 |
| 2 |
(6) |
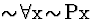 |
2,5 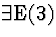 |
| 1 |
(7) |
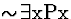 |
1,6 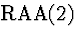 |
Comment: Note that
our rules allow you to ``discharge'' a primary assumption in an RAA proof
(line (5)). What this indicates here is simply that the assumption
in question is incompatible with the sentences indicated in the assumption
set. However, this feature of the system might seem unintuitive if
you (as I) like to think of discharged assumptions as temporary
assumptions that have been discarded because they have served their purpose
(in RAA, 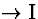 ,
or
,
or 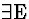 ).
Consequently, people of this mindset might prefer the following proof,
in which a copy of the primary assumption
).
Consequently, people of this mindset might prefer the following proof,
in which a copy of the primary assumption 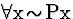 is
explicitly assumed (line (3) for RAA and later discharged (line 6).
is
explicitly assumed (line (3) for RAA and later discharged (line 6).
| 1 |
(1) |
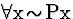 |
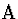 |
| 2 |
(2) |
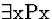 |
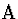 (for
(for 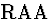 ) ) |
| 3 |
(3) |
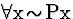 |
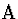 (for
(for 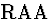 ) ) |
| 4 |
(4) |
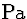 |
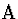 (for
(for 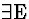 ) ) |
| 3 |
(5) |
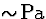 |
3 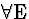 |
| 4 |
(6) |
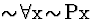 |
4,5 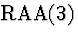 |
| 2 |
(7) |
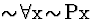 |
2,6 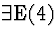 |
| 1 |
(8) |
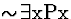 |
1,7 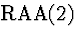 |
Comment: There
are a number of valid sequents that, roughly, show how quantifiers are
effected by altering their scopes. These are called Confinement
rules.
| (S134) |
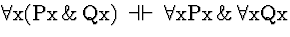 |
Confinement |
|
|
|
| |
|
|
|
|
|
| (S135) |
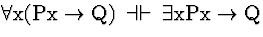 |
Conf |
|
|
|
| |
|
|
|
|
|
| (S136) |
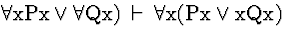 |
Conf |
|
|
|
| |
|
|
|
|
|
| (S137) |
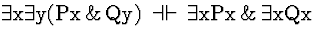 |
Conf |
|
|
|
| |
|
|
|
|
|
| (S138) |
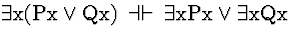 |
Conf |
|
|
|
| |
|
|
|
|
|
| (S139) |
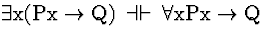 |
Conf |
|
|
|
| |
|
|
|
|
|
| (S140) |
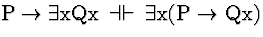 |
Conf |
|
|
|
| |
|
|
|
|
|
| (S141) |
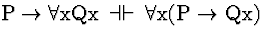 |
Conf |
|
|
|
Comment: The QE
rules and the Confinement rules indicate that any sentence may be converted
into an equivalent sentence in which no connective is outside the scope
of any quantifier in the formula. Such a sentence, called a prenex
sentence, has all its quantifiers in a row at the beginning of the sentence.
About
this document ...
Chris Menzel
22 April 1998