Comment: Filling in a truth table can be thought of as an algorithm (a definite precedure) for finding invalidating assignments: Fill in each row until your either find an invalidating assignment or you fill in all the rows. The indirect truth table method is a more efficient algorithm.
Example: an invalid sequent
Since our goal is to try
to find an invalidating assignment, we start by putting T's under the main
connective of each premise of the sequent and an F under the main connective
of the conclusion (or just under the sentence letter itself if the wff
in question is atomic).
Because the only way for
a conditional to be false is for the antecedent to be true and the consequent
false, we know that 
must be true and 
must be false in order for the conclusion of our sequent to be false. So
we add that information to our table:
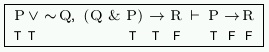
Now, notice that the first
premise is now guaranteed to be true, given that
is true (because all it takes for a disjunction to be true is for both
disjuncts to be true). But notice that the second premise has a false consequent.
Since we need it to be true, we must make the antecedent false as well
(since a conditional with a false antecedent is true).
is already true in the antecedent, but we have yet to assign a truth value
to .
Hence, we are still free to assign it whatever we want, and if we assign
it F, then, because it is a conjunction, the antecedent of the premise
will be false, making the entire premise true, as we want. So let's add
that information to the table as well:
All that's left to do is
to fill in the truth value of 
:
And so we end up with is,
basically, a complete row of a truth table on which the premises of the
sequent are true and the consequent is false, i.e., a row representing
an invalidating assignment, namely, :T :F 
:F.
So we have demonstrated, in a much more efficient fashion, that the sequent
is invalid.
Example: a valid sequent
As above, we start by placing
a T under the main connective of each premise, and an F under the conclusion:
As before, we know that
must be true and
must be false in order for the conclusion of the sequent to be false. And
since
is true we also know that 
must be false. So we add all of that information to our table:
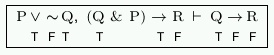
Looking at the second premise
here, we see that we are going to have to make
false in order for the entire conditional to be true. So let us add that
information to the table:
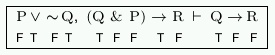
But notice that we have ended
up with both
and
false, which means that the disjunction 
is false, contrary to our initial assumption that it is true. So our assumption
that we could make the premises of the sequent true and the consequent
false proved to be false. That is, it turned out to be impossible to come
up with an invalidating assigment for the sequent. Hence, the sequent is
valid.
Example: a harder case
Now we'll look at a harder -- actually, no harder, just longer -- case. What makes it harder is simply that, once we fill in our initial T's and F's under the main connectives of the premises and conclusion, we have several choices as to what to do next.
In the sequents above, there was three ways to make each premise true, but only one way to make the conclusion false, which have us immediate truth values for two of the sentence letters. The problem with the present sequent is that there are three ways to make each premise true and three ways to make the conclusion false. So we just have start with one of the wffs in the sequent (it doesn't matter which) and pick one of the three ways to make it false. If it doesn't yield an invalidating assignment, then we try another until either we find an invalidating assignment or we run out of possibilities.
So suppose we just start
with conclusion again. There are three ways to make 
false: both 
and 
can be false, or one can be true and the other false. Let's try the case
where both are false, and add that information to the table:
Notice now that the consequent
of the third premise is false. That means, again, that in order to make
the entire premise true, we have to make the antecedent 
false. But, since the antecedent is a disjunction, that requires us to
make disjuncts
and
false. So let us add that information to the table:
We can now calculate the
values of 
and 
,
so let's do that:
Since the both of the first two premises have false consequents, we know that their antecedents have to be false as well for those premises to be true:
But, of course, this is impossible;
if
is false, then 
has to true, and vice versa. So this attempt at an invalidating assignment
fails.
Now, recall that this attempt started with just one of three possible ways to make the conclusion of this sequent false. Hence, we have to try the other two and fail to find an invalidating assignment with both of them before we can conclude that the sequent is valid. That is, we must complete the following two indirect truth tables:
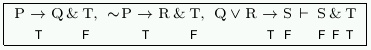
It is left as an exercise for the reader to determine whether either of these leads to an invalidating assignment.