 |
It is widely known that |
| T | ? |
| F | F |
Definition: A truth table for a connective * is a table that displays how the truth value of a sentence whose main connective is * is determined by the truth values of its immediate sentential components.
Definition: A connective * is truth functional if the truth value of any sentence whose main connective is * is completely determined by the truth values of its immediate sentential components.
Comment: We are only interested in constructing truth tables for connectives that are truth functional .
Example: ``It is widely known
that'' is not truth functional
|
It is widely known that |
| T | ? |
| F | F |
Comment: All of the
connectives introduced in Chapter 1 are truth functional.
|
 |
| T | F |
| F | T |
Comment: in order
for a negation
to be true,
must be false; and for
to be false,
must be true.
|
 |
 |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Comment: In order
for a conjunction
to be true, both
and
must both be true. Otherwise
is false.
|
|
 |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Comment: In order
for a disjunction to
be true, either
or
(possibly both) must be true. Thus,
is false if and only if both and
are false.
|
|
 |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Comment: In order
for a conditional to
be true, either
must be false or
must be true. Thus,
is false if and only if is
true and
is false.
Comment: If the antecedent
of a conditional
it false, then is
true regardless of the truth value of .
Similarly, if the consequent
is true, then
is true regardless of the truth value of .
(Cp. the derived rules False Antecedent (
)
and True Consequent (
).
|
|
 |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Comment: In order
for a biconditional to
be true,
and
must have the same truth value, i.e., either both
and
are true or both are false. Otherwise,
is false.
Definition: A truth table for a sentence
is a table that displays how the truth value of
is determined by the truth values of its constituent sentence letters.
Comment: The truth
table for any sentence is
constructed in accordance with the truth tables for connectives, starting
with the smallest sub-sentences of
(i.e., the ones whose immediate sentential components are sentence letters)
and working ``upwards''. The column for a given component of a sentence
(other than the sentence letters) is placed under that component's main
connective.
Example
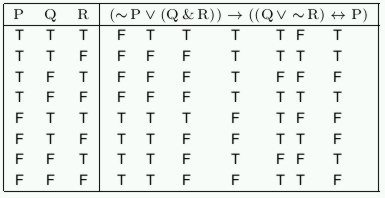
Comment: If a sentence contains n distinct constituent sentence letters (types, not tokens), then there are 2n rows in its truth table.
Definition: A sentence
in given a truth table is said to be true on a row of the truth
table if a T occurs below its main connective on that row. Otherwise it
is said to be false on that row.
Example
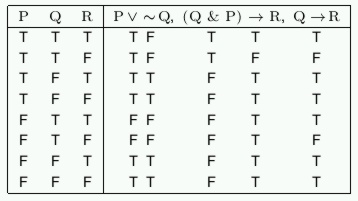
Definition: A truth value assignment for a set
of sentences 
is an assignment of a single truth value to each constituent sentence letter
occurring in the sentences 
,
..., 
(and
possibly also to other sentence letters as well).
Comment: If n=1,
i.e., for singleton sets 
,we
will usually just talk about truth value assignments for the sentence rather
than the set singleton set .
Comment: Each row
of a truth table for a set of sentences
corresponds to a truth value assignment for that set. Furthermore, every
(relevant) truth value assignment for the set is represented by some row
of the truth table for the set.
Comment: We will occasionally
indicate a truth value assignment for a sentence (e.g., in the QuizMaster)
with the notation 
sentence
letter
: truth
value.
So, e.g., the truth value assignment assigning T to P
and Q and F to R
would be indicated in this manner by P:T
Q:T R:F.
Definition: A sentence
is said to be true on a given truth value assignment if it is true
on the the row corresponding to that assignment in the truth table for .