@ = 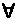
$
= 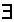
@ = 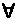
$
= 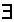
S77: $x(Gx&~Fx), @x(Gx->Hx) |- $x(Hx&~Fx)
| 1 | (1) | $x(Gx&~Fx) | a |
| 2 | (2) | @x(Gx->Hx) | a |
| 3 | (3) | Ga&~Fa | a |
| 2 | (4) | Ga->Ha | 2 @E |
| 3 | (5) | Ga | 3 &E |
| 3 | (6) | ~Fa | 3 &E |
| 2,3 | (7) | Ha | 4,5 ->E |
| 2,3 | (8) | Ha&~Fa | 6,7 &I |
| 2,3 | (9) | $x(Hx&~Fx) | 8 $I |
| 1,2 | (10) | $x(Hx&~Fx) | 1,9 $E(3) |
S78
$x(Gx&Fx), @x(Fx->~Hx) |- $x~Hx
| 1 | (1) | $x(Gx&Fx) | a |
| 2 | (2) | @x(Fx->~Hx) | a |
| 3 | (3) | Ga&Fa | a |
| 3 | (4) | Fa | 3 &E |
| 2 | (5) | Fa->~Ha | 2 @E |
| 2,3 | (6) | ~Ha | 4,5 @E |
| 2,3 | (7) | $x~Hx | 6 $I |
| 1,2 | (8) | $x~Hx | 1,7 $E(3) |
S79: @x(Gx->~Fx), @x(~Fx->~Hx) |- @x(Gx->~Hx)
| 1 | (1) | @x(Gx->~Fx) | a |
| 2 | (2) | @x(~Fx->~Hx) | a |
| 1 | (3) | Ga->~Fa | 1 @E |
| 2 | (4) | ~Fa->~Ha | 2 @E |
| 1,2 | (5) | Ga->~Ha | 3,4 HS |
| 1,2 | (6) | @x(Gx->~Hx) | 5 @I |
S80: @x(Gx->$y(Fy&Hy)) |- @x~Fx->~$zGz
| 1 | (1) | @x(Gx->$y(Fy&Hy)) | a |
| 2 | (2) | @x~Fx | a (for ->I) |
| 3 | (3) | $zGz | a (for RAA) |
| 4 | (4) | Ga | a (for $E) |
| 1 | (5) | Ga->$y(Fy&Hy) | 1 @E |
| 1,4 | (6) | $y(Fy&Hy) | 4,5 ->E |
| 7 | (7) | Fb&Hb | a |
| 7 | (8) | Fb | 7 &E |
| 2 | (9) | ~Fb | 2 @E |
| 2,7 | (10) | ~$zGz | 8,9 RAA(3) |
| 1,2,4 | (11) | ~$zGz | 6,10 $E(7) |
| 1,2,3 | (12) | ~$zGz | 3,11 $E(4) |
| 1,2 | (13) | ~$zGz | 3,12 RAA(3) |
| 1 | (14) | @x~Fx->~$zGz | 13 ->I(2) |
S81: @x(Gx->(Hx&Jx)), @x((Fx v ~Jx)->Gx) |- @x(Fx->Hx)
| 1 | (1) | @x(Gx->(Hx&Jx)) | a |
| 2 | (2) | @x((Fx v ~Jx)->Gx) | a |
| 1 | (3) | Ga->(Ha&Ja) | 1 @E |
| 2 | (4) | (Fa v ~Ja)->Ga | 2 @E |
| 5 | (5) | Fa | a |
| 5 | (6) | Fa v ~Ja | 5 vI |
| 2,5 | (7) | Ga | 4,6 ->E |
| 1,2,5 | (8) | Ha&Ja | 3,7 ->E |
| 1,2,5 | (9) | Ha | 8 &E |
| 1,2 | (10) | Fa->Ha | 9 ->I(5) |
| 1,2 | (11) | @x(Fx->Hx) | 10 @I |
S82: @x((Gx&Kx)<->Hx), ~$x(Fx&Gx) |- @x~(Fx&Hx)
| 1 | (1) | @x((Gx&Kx)<->Hx) | a |
| 2 | (2) | ~$x(Fx&Gx) | a |
| 3 | (3) | Fa&Ha | a |
| 3 | (4) | Ha | 3 &E |
| 1 | (5) | (Ga&Ka)<->Ha | 1 @E |
| 1,3 | (6) | Ga&Ka | 4,5 BP |
| 1,3 | (7) | Ga | 6 &E |
| 3 | (8) | Fa | 3 &E |
| 1,3 | (9) | Fa&Ga | 7,8 &I |
| 1,3 | (10) | $x(Fx&Gx) | 9 $I |
| 1,2 | (11) | ~(Fa&Ha) | 2,10 RAA(3) |
| 1,2 | (12) | @x~(Fx&Hx) | 11 @I |
S83: @x(Gx->Hx), $x((Fx&Gx)&Mx) |- $x(Fx&(Hx&Mx))
| 1 | (1) | @x(Gx->Hx) | a |
| 2 | (2) | $x((Fx&Gx)&Mx) | a |
| 3 | (3) | (Fa&Ga)&Ma | a |
| 3 | (4) | Fa&Ga | 3 &E |
| 3 | (5) | Ma | 3 &E |
| 3 | (6) | Ga | 4 &E |
| 3 | (7) | Fa | 4 &E |
| 1 | (8) | Ga->Ha | 1 @E |
| 1,3 | (9) | Ha | 6,8 ->E |
| 1,3 | (10) | Ha&Ma | 5,9 &I |
| 1,3 | (11) | Fa&(Ha&Ma) | 7,10 &I |
| 1,3 | (12) | $x(Fx&(Hx&Mx)) | 11 $I |
| 1,2 | (13) | $x(Fx&(Hx&Mx)) | 2,12 $E(3) |
S84: @x(~Gx v ~Hx), @x((Jx->Fx)->Hx) |- ~$x(Fx&Gx)
| 1 | (1) | @x(~Gx v ~Hx) | a |
| 2 | (2) | @x((Jx->Fx)->Hx) | a |
| 3 | (3) | $x(Fx&Gx) | a |
| 4 | (4) | Fa&Ga | a |
| 4 | (5) | Fa | 4 &E |
| 4 | (6) | Ga | 4 &E |
| 1 | (7) | ~Ga v ~Ha | 1 @E |
| 1 | (8) | Ga->~Ha | 7 v-> |
| 1,4 | (9) | ~Ha | 6,8 ->E |
| 2 | (10) | (Ja->Fa)->Ha | 2 @E |
| 1,2,4 | (11) | ~(Ja->Fa) | 9,10 MTT |
| 1,2,4 | (12) | Ja&~Fa | 11 Neg-> |
| 1,2,4 | (13) | ~Fa | 12 &E |
| 1,2,4 | (14) | ~$x(Fx&Gx) | 5,13 RAA(3) |
| 1,2,3 | (15) | ~$x(Fx&Gx) | 3,14 $E(4) |
| 1,2 | (16) | ~$x(Fx&Gx) | 3,15 RAA(3) |
S85: ~$x(~Gx&Hx), @x(Fx->~Hx) |- @x((Fx v ~Gx)->~Hx)
| 1 | (1) | ~$x(~Gx&Hx) | a |
| 2 | (2) | @x(Fx->~Hx) | a |
| 3 | (3) | Fa v ~Ga | a |
| 4 | (4) | Ha | a |
| 2 | (5) | Fa->~Ha | 2 @E |
| 2,4 | (6) | ~Fa | 4,5 MTT |
| 2,3,4 | (7) | ~Ga | 3,6 vE |
| 2,3,4 | (8) | ~Ga&Ha | 4,7 &I |
| 2,3,4 | (9) | $x(~Gx&Hx) | 8 $I |
| 1,2,3 | (10) | ~Ha | 1,9 RAA(4) |
| 1,2 | (11) | (Fa v ~Ga)->~Ha | 10 ->I(3) |
| 1,2 | (12) | @x((Fx v ~Gx)->~Hx) | 11 @I |
S86: @x~(Gx&Hx), $x(Fx&Gx) |- $x(Fx&~Hx)
| 1 | (1) | @x~(Gx&Hx) | a |
| 2 | (2) | $x(Fx&Gx) | a |
| 3 | (3) | Fa&Ga | a |
| 1 | (4) | ~(Ga&Ha) | 1 @E |
| 3 | (5) | Ga | 3 &E |
| 1 | (6) | ~Ga v ~Ha | 4 DM |
| 1,3 | (7) | ~Ha | 5,6 vE |
| 3 | (8) | Fa | 3 &E |
| 1,3 | (9) | Fa&~Ha | 7,8 &I |
| 1,3 | (10) | $x(Fx&~Hx) | 9 $I |
| 1,2 | (11) | $x(Fx&~Hx) | 2,10 $E(3) |
S87: $x(Fx&~Hx), ~$x(Fx&~Gx), |- ~@x(Gx->Hx)
| 1 | (1) | $x(Fx&~Hx) | a |
| 2 | (2) | ~$x(Fx&~Gx) | a |
| 3 | (3) | @x(Gx->Hx) | a |
| 4 | (4) | Fa&~Ha | a |
| 3 | (5) | Ga->Ha | 3 @E |
| 4 | (6) | ~Ha | 4 &E |
| 3,4 | (7) | ~Ga | 5,6 MTT |
| 4 | (8) | Fa | 4 &E |
| 3,4 | (9) | Fa&~Ga | 7,8 &I |
| 3,4 | (10) | $x(Fx&~Gx) | 9 $I |
| 2,4 | (11) | @x(Gx->Hx) | 2,10 RAA(3) |
| 1,2 | (12) | @x(Gx->Hx) | 1,11 $E(3) |
S88: @x(Hx->(Hx&Gx)), $x(~Gx&Fx) |- $x(Fx&~Hx)
| 1 | (1) | @x(Hx->(Hx&Gx)) | a |
| 2 | (2) | $x(~Gx&Fx) | a |
| 3 | (3) | ~Ga&Fa | a |
| 1 | (4) | Ha->(Ha&Ga) | 1 @E |
| 3 | (5) | ~Ga | 3 &E |
| 3 | (6) | ~Ha v ~Ga | 5 vI |
| 3 | (7) | ~(Ha&Ga) | 6 DM |
| 1,3 | (8) | ~Ha | 4,7 MTT |
| 3 | (9) | Fa | 3 &E |
| 1,3 | (10) | Fa&~Ha | 8,9 &I |
| 1,3 | (11) | $x(Fx&~Hx) | 10 $I |
| 1,2 | (12) | $x(Fx&~Hx) | 2,11 $E(3) |
S89: @x(Hx->~Gx), ~$x(Fx&~Gx) |- @x~(Fx&Hx)
| 1 | (1) | @x(Hx->~Gx) | a |
| 2 | (2) | ~$x(Fx&~Gx) | a |
| 3 | (3) | Fa&~Ga | a |
| 3 | (4) | $x(Fx&~Gx) | 3 $I |
| 2 | (5) | ~(Fa&~Ga) | 2,4 RAA(3) |
| 1 | (6) | Ha->~Ga | 1 @E |
| 2 | (7) | Fa->Ga | 5 Neg-> |
| 1 | (8) | Ga->~Ha | 6 Trans |
| 1,2 | (9) | Fa->~Ha | 7,8 HS |
| 1,2 | (10) | ~(Fa&Ha) | 9 Neg-> |
| 1,2 | (11) | @x~(Fx&Hx) | 10 @I |
S90: @x(Fx<->Gx) |- @xFx <-> @xGx
| 1 | (1) | @x(Fx<->Gx) | a |
| 2 | (2) | @xFx | a |
| 2 | (3) | Fa | 2 @E |
| 1 | (4) | Fa<->Ga | 1 @E |
| 1,2 | (5) | Ga | 3,4 BP |
| 1,2 | (6) | @xGx | 5 @I |
| 1 | (7) | @xFx -> @xGx | 6 ->I(2) |
| 8 | (8) | @xGx | a |
| 8 | (9) | Ga | 8 @E |
| 1 | (10) | Fa<->Ga | 1 @E |
| 1,8 | (11) | Fa | 9,10 BP |
| 1,8 | (12) | @xFx | 11 @I |
| 1 | (13) | @xGx->@xFx | 12 ->I(8) |
| 1 | (14) | @xFx <-> @xGx | 7,13 <->I |
S91: $xFx->@y(Gy->Hy), $xJx->$xGx |- $x(Fx&Jx) -> $zHz
| 1 | (1) | $xFx->@y(Gy->Hy) | a |
| 2 | (2) | $xJx->$xGx | a |
| 3 | (3) | $x(Fx&Jx) | a |
| 4 | (4) | Fa&Ja | a |
| 4 | (5) | Fa | 4 &E |
| 4 | (6) | $xFx | 5 $I |
| 1,4 | (7) | @y(Gy->Hy) | 1,6 ->E |
| 4 | (8) | Ja | 4 &E |
| 4 | (9) | $xJx | 8 $I |
| 2,4 | (10) | $xGx | 2,9 ->E |
| 11 | (11) | Gb | a |
| 1,4 | (12) | Gb->Hb | 7 @E |
| 1,4,11 | (13) | Hb | 11,12 ->E |
| 1,4,11 | (14) | $zHz | 13 $I |
| 1,2,4 | (15) | $zHz | 10,14 $E(11) |
| 1,2,3 | (16) | $zHz | 3,15 $E(4) |
| 1,2 | (17) | $x(Fx&Jx) -> $zHz | 16 ->I(3) |
S92: $xFx v $xGx, @x(Fx->Gx) |- $xGx
| 1 | (1) | $xFx v $xGx | a |
| 2 | (2) | @x(Fx->Gx) | a |
| 3 | (3) | ~$xGx | a |
| 1,3 | (4) | $xFx | 1,3 vE |
| 5 | (5) | Fa | a |
| 2 | (6) | Fa->Ga | 2 @E |
| 2,5 | (7) | Ga | 5,6 ->E |
| 2,5 | (8) | $xGx | 7 $I |
| 1,2,3 | (9) | $xGx | 4,8 $E(5) |
| 1,2 | (10) | $xGx | 3,9 RAA(3) |
S93: @x(Fx->~Gx) |- ~$x(Fx&Gx)
| 1 | (1) | @x(Fx->~Gx) | a |
| 2 | (2) | $x(Fx&Gx) | a |
| 3 | (3) | Fa&Ga | a |
| 1 | (4) | Fa->~Ga | 1 @E |
| 1 | (5) | ~(Fa&Ga) | 4 Neg-> |
| 1,3 | (6) | ~$x(Fx&Gx) | 3,5 RAA(2) |
| 1,2 | (7) | ~$x(Fx&Gx) | 2,6 $E(3) |
| 1 | (8) | ~$x(Fx&Gx) | 2,7 RAA(2) |
S94: @x((Fx v Hx)->(Gx&Kx)), ~@x(Kx&Gx) |- $x~Hx
| 1 | (1) | @x((Fx v Hx)->(Gx&Kx)) | a |
| 2 | (2) | ~@x(Kx&Gx) | a |
| 3 | (3) | ~$x~Hx | a |
| 4 | (4) | ~Ha | a |
| 4 | (5) | $x~Hx | 4 $I |
| 3 | (6) | Ha | 3,5 RAA(4) |
| 1 | (7) | (Fa v Ha)->(Ga & Ka) | 1 @E |
| 3 | (8) | Fa v Ha | 6 vI |
| 1,3 | (9) | Ga & Ka | 7,8 ->E |
| 1,3 | (10) | Ka & Ga | 9 &Comm |
| 1,3 | (11) | @x(Kx&Gx) | 10 @I |
| 1,2 | (12) | $x~Hx | 2,11 RAA(3) |
S95: @x((Fx&Gx)->Hx), Ga & @xFx |- Fa & Ha
| 1 | (1) | @x((Fx&Gx)->Hx) | a |
| 2 | (2) | Ga & @xFx | a |
| 2 | (3) | Ga | 2 &E |
| 2 | (4) | @xFx | 2 &E |
| 2 | (5) | Fa | 4 @E |
| 1 | (6) | (Fa & Ga)->Ha | 1 @E |
| 2 | (7) | Fa & Ga | 3,5 &I |
| 1,2 | (8) | Ha | 6,7 ->E |
| 1,2 | (9) | Fa & Ha | 5,8 &I |
S96: @x(Fx<->@yGy) |- @xFx v @x~Fx
| 1 | (1) | @x(Fx<->@yGy) | a |
| 2 | (2) | ~@x~Fx | a |
| 3 | (3) | ~$xFx | a |
| 4 | (4) | Fa | a |
| 4 | (5) | $xFx | 4 $I |
| 3 | (6) | ~Fa | 3,5 RAA(4) |
| 3 | (7) | @x~Fx | 6 @I |
| 2 | (8) | $xFx | 2,7 RAA(3) |
| 9 | (9) | Fa | a |
| 1 | (10) | Fa<->@yGy | 1 @E |
| 1,9 | (11) | @yGy | 9,10 BP |
| 1 | (12) | Fb<->@yGy | 1 @E |
| 1,9 | (13) | Fb | 11,12 BP |
| 1,9 | (14) | @xFx | 13 @I |
| 1,2 | (15) | @xFx | 8,14 $E(9) |
| 1 | (16) | ~@x~Fx -> @xFx | 15 ->I(2) |
| 1 | (17) | @x~Fx v @xFx | 16 v-> |
| 1 | (18) | @xFx v @x~Fx | 17 v Comm |
S97: @y(Fa->($xGx->Gy)), @x(Gx->Hx), @x(~Jx->~Hx) |- $x~Jx -> (~Fa v @x~Gx)
| 1 | (1) | @y(Fa->($xGx->Gy)) | a |
| 2 | (2) | @x(Gx->Hx) | a |
| 3 | (3) | @x(~Jx->~Hx) | a |
| 4 | (4) | $x~Jx | a |
| 5 | (5) | Fa | a |
| 6 | (6) | ~Jb | a |
| 2 | (7) | Gb->Hb | 2 @E |
| 1 | (8) | Fa->($xGx->Gb) | 1 @E |
| 3 | (9) | ~Jb->~Hb | 3 @E |
| 3,6 | (10) | ~Hb | 6,9 ->E |
| 2,3,6 | (11) | ~Gb | 7,10 MTT |
| 1,5 | (12) | $xGx->Gb | 5,8 ->E |
| 1,2,3,5,6 | (13) | ~$xGx | 11,12 MTT |
| 1,2,3,4,5 | (14) | ~$xGx | 4, 13 $E(6) |
| 15 | (15) | Gc | a |
| 15 | (16) | $xGx | 15 $I |
| 1,2,3,4,5 | (17) | ~Gc | 14,16 RAA(15) |
| 1,2,3,4,5 | (18) | @x~Gx | 17 @I |
| 1,2,3,4 | (19) | Fa->@x~Gx | 18 ->I(5) |
| 1,2,3,4 | (20) | ~Fa v @x~Gx | 19 v-> |
| 1,2,3 | (21) | $x~Jx -> (~Fa v @x~Gx) | 20 ->I(4) |
S98: @x(Dx->Fx) |- @z(Dz->(@y(Fy->Gy)->Gz))
| 1 | (1) | @x(Dx->Fx) | a |
| 2 | (2) | Da | a |
| 3 | (3) | @y(Fy->Gy) | a |
| 1 | (4) | Da->Fa | 1 @E |
| 3 | (5) | Fa->Ga | 3 @E |
| 1,2 | (6) | Fa | 2,4 ->E |
| 1,2,3 | (7) | Ga | 5,6 ->E |
| 1,2 | (8) | @y(Fy->Gy)->Ga | 7 ->I(3) |
| 1 | (9) | Da->(@y(Fy->Gy)->Ga) | 8 ->I(2) |
| 1 | (10) | @z(Dz->(@y(Fy->Gy)->Gz)) | 9 @I |
S99: $xFx<->@y((FyvGy)->Hy), $xHx, ~@z~Fz |- $x(Fx&Hx)
| 1 | (1) | $xFx<->@y((FyvGy)->Hy) | a |
| 2 | (2) | $xHx | a |
| 3 | (3) | ~@z~Fz | a |
| 4 | (4) | ~$xFx | a |
| 5 | (5) | Fa | a |
| 5 | (6) | $xFx | 5 $I |
| 4 | (7) | ~Fa | 4,6 RAA(5) |
| 4 | (8) | @z~Fz | 7 @I |
| 3 | (9) | $xFx | 3,8 RAA(4) |
| 1,3 | (10) | @y((FyvGy)->Hy) | 1,9 ->E |
| 11 | (11) | Fa | a |
| 1,3 | (12) | (FavGa)->Ha | 10 @E |
| 11 | (13) | FavGa | 11 vI |
| 1,3,11 | (14) | Ha | 12,13 ->E |
| 1,3,11 | (15) | Fa&Ha | 11,14 &I |
| 1,3,11 | (16) | $x(Fx&Hx) | 15 $I |
| 1,3 | (17) | $x(Fx&Hx) | 9,16 $E(11) |
S100: @xFx |- ~$xGx<->~($x(Fx&Gx)&@y(Gy->Fy))
| 1 | (1) | @xFx | a |
| 2 | (2) | $xGx | a |
| 3 | (3) | Ga | a |
| 1 | (4) | Fa | 1 @E |
| 1,3 | (5) | Fa&Ga | 3,4 &I |
| 1,3 | (6) | $x(Fx&Gx) | 5 $I |
| 1,2 | (7) | $x(Fx&Gx) | 2,6 $E(3) |
| 1 | (8) | Fb | 1 @E |
| 1 | (9) | Gb->Fb | 8 TC |
| 1 | (10) | @y(Gy->Fy) | 9 @I |
| 1,2 | (11) | $x(Fx&Gx)&@y(Gy->Fy) | 7,10 &I |
| 1 | (12) | $xGx->$x(Fx&Gx)&@y(Gy->Fy) | 11 ->I(2) |
| 13 | (13) | $x(Fx&Gx)&@y(Gy->Fy) | a |
| 13 | (14) | $x(Fx&Gx) | 13 &E |
| 15 | (15) | Fc&Gc | a |
| 15 | (16) | Gc | 15 &E |
| 15 | (17) | $xGx | 16 $I |
| 13 | (18) | $xGx | 14,17 $E(15) |
| (19) | ($x(Fx&Gx)&@y(Gy->Fy))->$xGx | 18 ->I(13) | |
| 1 | (20) | ($x(Fx&Gx)&@y(Gy->Fy))<->$xGx | 12,19 <->I |
| 1 | (21) | ~$xGx<->~($x(Fx&Gx)&@y(Gy->Fy)) | 20 BiTrans |
S101: @x($yFyx->@zFxz) |- @y@x(Fyx->Fxy)
| 1 | (1) | @x($yFyx->@zFxz) | a |
| 1 | (2) | $yFya->@zFaz | 1 @E |
| 3 | (3) | Fba | a |
| 3 | (4) | $yFya | 3 $I |
| 1,3 | (5) | @zFaz | 2,4 ->E |
| 1,3 | (6) | Fab | 5 @E |
| 1 | (7) | Fba->Fab | 6 ->I(3) |
| 1 | (8) | @x(Fbx->Fxb) | 7 @I |
| 1 | (9) | @y@x(Fyx->Fxy) | 8 @I |
S102: $x(Fx&@yGxy), @x@y(Gxy->Gyx) |- $x(Fx&@yGyx)
| 1 | (1) | $x(Fx&@yGxy) | a |
| 2 | (2) | @x@y(Gxy->Gyx) | a |
| 3 | (3) | Fa&@yGay | a |
| 2 | (4) | @y(Gay->Gya) | 2 @E |
| 2 | (5) | Gab->Gba | 4 @E |
| 3 | (6) | Fa | 3 &E |
| 3 | (7) | @yGay | 3 &E |
| 3 | (8) | Gab | 7 @E |
| 2,3 | (9) | Gba | 5,8 ->E |
| 2,3 | (10) | @yGya | 9 @I |
| 2,3 | (11) | Fa&@yGya | 6,10 &I |
| 2,3 | (12) | $x(Fx&@yGyx) | 11 $I |
| 1,2 | (13) | $x(Fx&@yGyx) | 1,12 $E(3) |
S103: $x~@y(Gxy->Gyx) |- $x$y(Gxy&~Gyx)
| 1 | (1) | $x~@y(Gxy->Gyx) | a |
| 2 | (2) | ~$x$y(Gxy&~Gyx) | a |
| 3 | (3) | ~@y(Gay->Gya) | a |
| 4 | (4) | Gab&~Gba | a |
| 4 | (5) | $x(Gax&~Gxa) | 4 $I |
| 4 | (6) | $x$y(Gxy&~Gyx) | 5 $I |
| 2 | (7) | ~(Gab&~Gba) | 2,6 RAA(4) |
| 2 | (8) | Gab->Gba | 7 Neg-> |
| 2 | (9) | @y(Gay->Gya) | 8 @I |
| 3 | (10) | $x$y(Gxy&~Gyx) | 3,9 RAA(2) |
| 1 | (11) | $x$y(Gxy&~Gyx) | 1,10 $E(3) |
S104: @x(Gx->@y(Fy->Hxy)), $x(Fx&@z~Hxz) |- ~@xGx
| 1 | (1) | @x(Gx->@y(Fy->Hxy)) | a |
| 2 | (2) | $x(Fx&@z~Hxz) | a |
| 3 | (3) | @xGx | a |
| 4 | (4) | Fa&@z~Haz | a |
| 4 | (5) | Fa | 4 &E |
| 4 | (6) | @z~Haz | 4 &E |
| 3 | (7) | Ga | 3 @E |
| 1 | (8) | Ga->@y(Fy->Hay) | 1 &E |
| 1,3 | (9) | @y(Fy->Hay) | 7,8 ->E |
| 1,3 | (10) | Fa->Haa | 9 @E |
| 1,3,4 | (11) | Haa | 5,10 ->E |
| 4 | (12) | ~Haa | 6 @E |
| 1,4 | (13) | ~@xGx | 11,12 RAA(3) |
| 1,2 | (14) | ~@xGx | 2,13 $E(4) |
S105: @x@y(Fxy->Gxy) |- @x(Fxx->$y(Gxy&Fyx))
| 1 | (1) | @x@y(Fxy->Gxy) | a |
| 2 | (2) | Faa | a |
| 1 | (3) | @y(Fay->Gay) | 1 @E |
| 1 | (4) | Faa->Gaa | 3 @E |
| 1,2 | (5) | Gaa | 2,4 ->E |
| 1,2 | (6) | Gaa&Faa | 2,5 &I |
| 1,2 | (7) | $x(Gay&Fya) | 6 $I |
| 1 | (8) | Faa->$x(Gay&Fya) | 7 ->I(2) |
| 1 | (9) | @x(Fxx->$y(Gxy&Fyx)) | 8 $I |